11.2 Convolve (2D & 3D)
Name
Convolve (2D/3D) -- Attribute that returns a filtered response.
Description
The input data is convolved with a three-dimensional kernel specified by Filter type and associated parameters. Lowpass, Laplacian, and Prewitt are well known filters in image processing.
Input Parameters
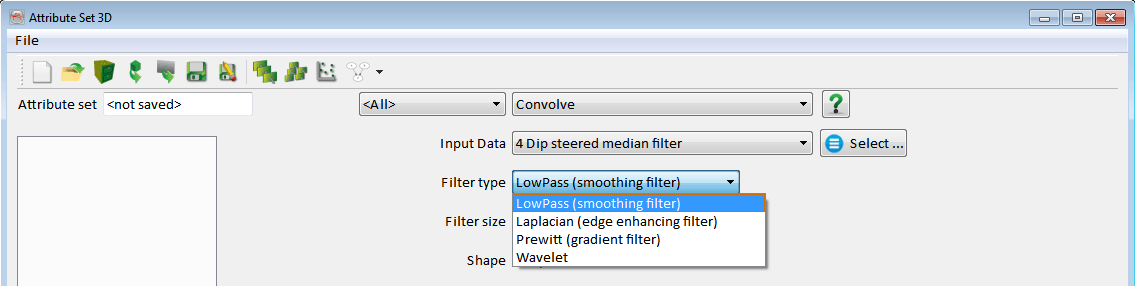
Lowpass

Lowpass is an arithmetic averaging filter which is used to smooth seismic data. The smoothness is determined by the Filter size. The shape parameter specifies whether the input samples are collected in a sphere or a cube centered around the evaluation point. The output is the sum of the sample values divided by the number of samples.
Laplacian
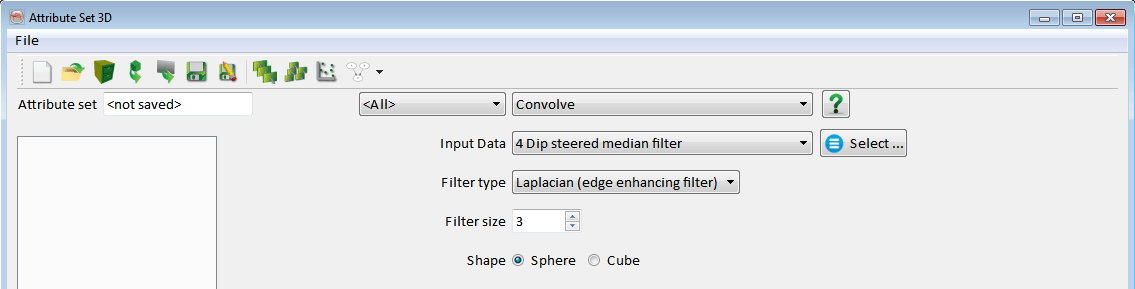
The Laplacian filter is an edge enhancement filter. The sharpness is determined by the Filter size. The shape parameter specifies the input samples to the filter. In a 3x3x3 Laplace filter, the output is calculated by multiplying the central sample value with 26 and subtracting all surrounding sample values. The convolution is characterized by the following kernel:
- (-1,-1,-1) (-1,-1 ,-1) (-1,-1,-1)
- (-1,-1,-1) (-1,+26,-1) (-1,-1,-1)
- (-1,-1,-1) (-1,-1 ,-1) (-1,-1,-1)
In case all sample values are equal and non-zero (either positive or negative), the effect of this operation is zero.
Prewitt
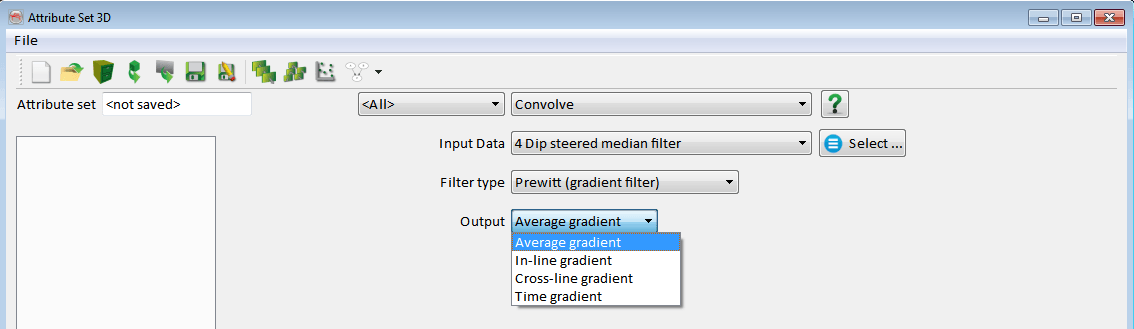
Prewitt is a contrast enhancement filter. This filter computes the gradient in different directions from a 3x3x3 input cube. The Output is returned in the specified direction (inline, crossline, or Z-plane). A 3x3x3 Prewitt kernel to calculate a horizontal gradient is given by:
- (1,0,-1) (1,0,-1) (1,0,-1)
- (1,0,-1) (1,0,-1) (1,0,-1)
- (1,0,-1) (1,0,-1) (1,0,-1)
Note that the inline gradient returns the difference in amplitude in the inline direction. This is best visualized on a crossline. Similarly, a crossline gradient is visualized best on an inline.
A 3x3x3 Prewitt kernel that returns the vertical gradient is given by:
- (-1,-1,-1) (-1,-1,-1) (-1,-1,-1)
- ( 0, 0, 0) ( 0, 0, 0) ( 0, 0, 0)
- ( 1, 1, 1) ( 1, 1, 1) ( 1, 1, 1)
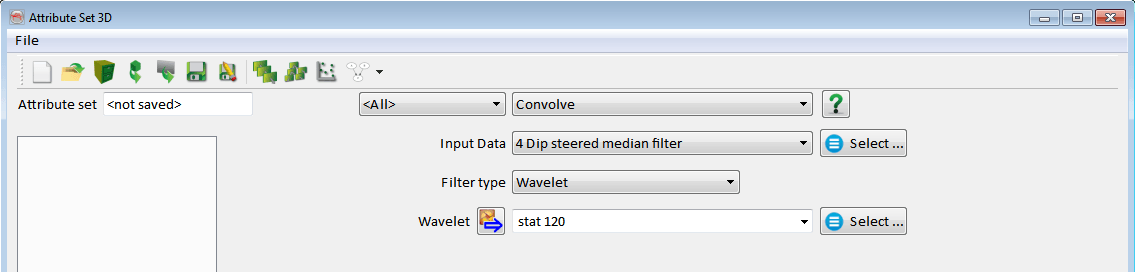
This option enables the user to convolve the data with a wavelet. In this context, a wavelet is the time series response of a filter. The wavelet should be imported into OpendTect first or it can also be created in OpendTect (From Wavelet management or ARKCLS Spectral blueing attribute).